O que é um gráfico logarítmico?
Um gráfico logarítmico é uma representação gráfica que emprega uma escala logarítmica, divergindo da escala linear convencional usada na maioria dos gráficos, onde os valores são espaçados uniformemente criando intervalos variados entre os valores.

Em contraste com a escala linear padrão comumente vista na maioria dos gráficos tradicionais, um gráfico logarítmico emprega uma escala logarítmica. Ao contrário das escalas lineares, que espaçam os valores uniformemente, as escalas logarítmicas criam lacunas variadas entre os valores, resultando em vantagens notáveis. Esta abordagem logarítmica é vantajosa quando se lida com conjuntos de dados que abrangem uma ampla gama de valores. Ela permite uma forma mais simplificada e eficiente de apresentar informações numéricas.
Os logaritmos introduzem um toque de não linearidade no mundo da representação matemática. Para compreender este conceito, considere os números 10 e 20 em comparação com 80 e 90. Numa escala logarítmica, os intervalos entre estes valores não são uniformes; em vez disso, aparecem intervalos uniformes entre números como 10 e 100 ou 60 e 600, pois representam um aumento consistente de 100% no valor.
Em essência, os logaritmos fornecem um método alternativo para expressar equações exponenciais. Esta abordagem permite a separação do expoente em um lado de uma equação. Por exemplo, a equação 42 = 16 pode ser transformada em “log de 16 na base 4 é igual a 2”, embora seja frequentemente afirmada como “log na base 4 de 16 é 2”. Neste caso, o logaritmo simbolizado como log emprega uma base 4 e é igual a 2.
Na equação y = base de log b (x), y simboliza o expoente ou potência necessária para elevar b para chegar a x. Esta representação logarítmica é fundamental em inúmeras aplicações matemáticas e científicas, proporcionando uma perspectiva distinta sobre a conexão entre os números e suas características exponenciais.
Como funciona o mecanismo de uma escala logarítmica?
Estabelecer uma escala é uma tarefa simples no domínio das funções lineares. Aqui, pode-se empregar incrementos inteiros onde cada etapa representa uma unidade de medida idêntica e imutável. Esta abordagem pode ser comparada à marcação de uma régua, onde o espaçamento entre cada marcação permanece consistentemente o mesmo. No entanto, quando o nosso foco muda para funções logarítmicas, a escala assume um caráter distinto, intrinsecamente ligado aos expoentes pelos quais um valor é aumentado.
Para obter uma visão mais profunda sobre isso, vamos contemplar um gráfico linear caracterizado por uma escala que aumenta em um. Neste cenário, cada passo para frente ou para trás no gráfico corresponde a uma mudança de uma unidade. Agora, compare isso com um gráfico logarítmico, em que a escala está enraizada nas potências de um número específico, muitas vezes considerado como 10.
Consideremos, por exemplo, uma situação hipotética em que a jornada de vendas de uma empresa começou com uma única venda em 1999. Notavelmente, esse número dobrou a cada ano subsequente até o ano de 2011. Se empregarmos uma escala linear neste contexto, ela representará os números brutos e absolutos das vendas registadas durante estes anos. Tal representação ilustra um aumento gradual, passando de uma única venda em 1999 para um valor de dois dígitos em 2000, e assim por diante.
No entanto, a adoção de uma escala logarítmica apresenta uma perspectiva totalmente distinta. Em vez de destacar os valores numéricos brutos, ela acentua o ritmo da mudança nas vendas ao longo deste período. Neste caso, ela enfatiza que os números de vendas duplicaram anualmente. Esta representação logarítmica nos dá um ponto de vista único que facilita o discernimento de padrões de crescimento exponencial com excepcional clareza.
Aprofundando-se nos fundamentos das escalas logarítmicas
As escalas logarítmicas representam um instrumento potente na visualização de dados, oferecendo um meio conciso e esclarecedor de transmitir grandes volumes de informações. Sua aplicabilidade abrange diversos campos, conferindo vantagens a analistas, pesquisadores e tomadores de decisão de diversas organizações. Uma sólida compreensão dos fundamentos das escalas logarítmicas é fundamental para aproveitar seu potencial de forma eficaz. Abaixo, apresentamos vários insights importantes a serem considerados:
Gráficos semilogarítmicos:
Um gráfico é "semilogarítmico" quando apenas um de seus eixos adota uma escala logarítmica. Esta abordagem permite uma representação versátil dos dados, em que um eixo adere à progressão linear habitual enquanto o outro adere ao princípio logarítmico. Esses gráficos revelam-se particularmente vantajosos quando confrontados com conjuntos de dados caracterizados por crescimento ou declínio exponencial ao longo de um eixo, enquanto mantêm uma trajetória linear ao longo do outro.
Gráficos log-log:
Em contraste, um gráfico "log-log" emprega escalas logarítmicas tanto para o eixo x quanto para o eixo y. Este tratamento logarítmico duplo revela-se inestimável ao examinar relações intrincadas entre variáveis que abrangem múltiplas ordens de magnitude. Ele pode revelar padrões e correlações intrincados que podem permanecer ocultos ao usar escalas lineares.
Restrições de escalas logarítmicas:
Embora as escalas logarítmicas ofereçam vários benefícios, elas possuem certas restrições. Uma limitação fundamental reside na sua incapacidade de representar números negativos ou zero. Esta limitação emana do princípio matemático central de que é inerentemente inatingível derivar estes valores elevando um número base a qualquer expoente. As escalas logarítmicas são adaptadas exclusivamente para valores positivos, tornando-as menos adequadas para conjuntos de dados que abrangem fenômenos com base em negatividade ou zero.
O valor logarítmico mínimo:
Dentro de uma escala logarítmica, o zero surge como o valor absoluto mais baixo concebível. No domínio dos logaritmos, isso equivale a um resultado de um, já que qualquer entidade numérica elevada à potência de zero invariavelmente resulta em um. Compreender esta faceta fundamental das escalas logarítmicas é importante ao interpretar dados estruturados neste formato específico.
Aplicações em diversos tipos de gráficos:
A adaptabilidade das escalas logarítmicas se estende a muitos tipos de gráficos, abrangendo desde gráficos de linhas e gráficos de barras até gráficos de pizza e gráficos de dispersão. Essa versatilidade capacita os analistas com a capacidade de visualizar e transmitir dados em vários contextos, facilitando assim uma compreensão mais profunda de tendências e fenômenos complexos.
A importância da integração de escalas logarítmicas na visualização de dados
A incorporação de escalas logarítmicas na representação de dados transcende a mera preferência; ela tem um peso significativo em nossa capacidade de transmitir informações complexas de maneira eficaz. As escalas logarítmicas surgem como ferramentas indispensáveis para enfrentar diversos desafios visuais, especialmente no tratamento de extensos conjuntos de dados, particularmente aqueles repletos de flutuações de valor substanciais. Elas garantem que os insights mais importantes sejam facilmente identificados.
Vamos considerar um cenário onde os dados são apresentados através de um gráfico de barras. Este conjunto de dados compreende numerosos valores, a maioria dentro de uma faixa relativamente estreita, enquanto outros poucos exibem valores significativamente elevados. Quando representadas numa escala linear, estas disparidades de magnitude podem criar obstáculos formidáveis para os observadores que se esforçam por extrair informações do gráfico.
As escalas logarítmicas resolvem esse dilema remodelando a representação visual dos dados. Veja por que elas têm importância:
Equalizam o impacto visual:
As escalas logarítmicas comprimem valores maiores e expandem os menores. Esse efeito de compressão e expansão nivela o campo visual para os pontos de dados de todo o gráfico, facilitando a diferenciação entre valores de magnitudes variadas. Consequentemente, os visualizadores podem compreender todo o espectro de dados sem a distração de valores discrepantes desproporcionalmente proeminentes.
Clareza em meio à complexidade:
Escalas logarítmicas em conjuntos de dados marcados por extensas variações introduzem estrutura ao que de outra forma poderia ser caótico. Elas organizam as informações de uma maneira que mantém a integridade de cada ponto de dados e, ao mesmo tempo, restringe o domínio de alguns valores discrepantes excepcionais. Essa organização é vital na investigação científica, na análise financeira e em outros domínios onde a precisão e a sutileza são fundamentais.
Facilitam a tomada de decisões embasadas:
A adoção de escalas logarítmicas promove a tomada de decisões embasadas. Ao eliminar as distorções causadas por valores extremos, os tomadores de decisão podem formular julgamentos sólidos baseados numa representação de dados mais precisa. As escalas logarítmicas aumentam a probabilidade de se tomar decisões acertadas, seja avaliando tendências de mercado, examinando fenômenos científicos ou qualquer outro campo que dependa de insights baseados em dados.
Aprimoram a comunicação de dados:
As escalas logarítmicas amplificam a capacidade comunicativa de tabelas e gráficos. Elas capacitam analistas de dados e pesquisadores a transmitir informações complexas de forma sucinta e compreensível. Isto se mostra particularmente vantajoso para apresentar descobertas para diversos públicos com diferentes níveis de perspicácia numérica.
Aproveite o poder da fórmula logarítmica
Aproveitar o potencial das escalas logarítmicas transcende um mero exercício numérico; é uma habilidade fundamental que permite navegar facilmente por extensos conjuntos de dados e decifrar conexões exponenciais complexas. Para empregar corretamente a fórmula logarítmica (y = log₁₀ (x)) e desvendar as sutilezas das escalas logarítmicas, siga estas etapas estratégicas:
Substituição da variável y:
Os logaritmos, em essência, oferecem um caminho simplificado para desvendar funções exponenciais intrincadas. Comece identificando a base, geralmente 10, e identifique o papel desempenhado pela variável y em seu contexto específico. Com esse entendimento, embarque na jornada para calcular a função e desvendar os segredos da variável x. Por exemplo, imagine que você tem a tarefa de representar graficamente uma função logarítmica e isso produz um valor y de 1.500. Implemente esse valor na fórmula conforme ilustrado abaixo:
1.500 = log₁₀(x)
Cálculo da função logarítmica:
Para descobrir a variável x, seu próximo passo envolve resolver a função logarítmica usando habilidades algébricas. Pensando no exemplo anterior com um valor y de 1.500, mude sua perspectiva para uma função exponencial e execute o cálculo da seguinte forma:
10^x = 1.500
Ao resolver o valor x, você terá a chave para definir a escala do seu gráfico.
Determinação da variável x:
Com as bases meticulosamente estabelecidas, agora é hora de deduzir a variável x. Esta variável determina essencialmente o incremento pelo qual cada passo na sua escala logarítmica avança ou regride. Voltando ao nosso exemplo anterior, resolver a equação 10^x = 1.500 produz um valor x de aproximadamente 3,18. Isto implica que, para cada mudança incremental no valor y, o valor x correspondente sofre um aumento de dez vezes em relação ao valor x anterior. Para ilustrar melhor, se o valor y ultrapassar 1.501, o valor x subirá para aproximadamente 31,76.
Esse processo triplo permite que você utilize com proficiência a fórmula logarítmica, decodifique relações exponenciais intrincadas, construa escalas significativas e avalie com confiança conjuntos de dados intrincados. Quer seus esforços girem em torno de exploração científica, modelagem financeira ou qualquer disciplina que exija precisão e percepção, o domínio da fórmula logarítmica equipa você com uma ferramenta formidável para decifrar a dinâmica dos dados numéricos.
A importância de adotar escalas logarítmicas
As escalas logarítmicas, uma ferramenta fundamental na representação de dados, fornecem um meio distinto de explicar as intrincadas variações presentes em uma ampla gama de fenômenos. Veja por que os indivíduos recorrem a escalas logarítmicas para obter informações sobre as complexidades do mundo que nos rodeia:
Sensibilidade a mudanças:
O nosso mundo raramente experimenta mudanças em incrementos uniformes. Tomemos a temperatura como exemplo. Considere a distinção entre 60 e 65 graus; é quase imperceptível. Em contraste, a diferença entre 105 graus e 110 graus é clara. Embora estas mudanças de temperatura possam parecer lineares quando colocadas numa escala, a nossa percepção delas está longe de ser linear. As escalas logarítmicas permitem-nos capturar com precisão estas diferenças discerníveis, comprimindo valores maiores e expandindo os menores. Elas fornecem uma representação de dados que se alinha ao nosso senso inato de mudança, tornando-a mais compreensível e intuitiva.
A escala Richter:
A escala Richter, uma ferramenta utilizada para medir a magnitude de terremotos, é uma ilustração clássica das escalas logarítmicas. Aqueles com experiência em eventos sísmicos entendem que distinguir entre um terremoto de magnitude 2,5 e 3,5 é um desafio, enquanto uma diferença de uma unidade entre 5,5 e 6,5 é inconfundível. A escala Richter revela a verdadeira natureza da liberação de energia sísmica, onde cada incremento de número inteiro significa não uma amplificação linear, mas uma amplificação de dez vezes na amplitude. Esta amplificação da mudança em níveis mais elevados sublinha a indispensabilidade das escalas logarítmicas na compreensão da atividade sísmica.
Medições de decibéis:
As escalas logarítmicas ocupam uma posição central no domínio do som. As medições de decibéis, frequentemente utilizadas em acústica, engenharia de som e telecomunicações, expressam a intensidade do som e as relações de potência de forma logarítmica. Esta abordagem permite-nos navegar pela extensa gama de percepção auditiva humana, abrangendo o espectro desde sussurros quase inaudíveis até sons estrondosamente altos. Isso é feito de uma maneira que reflete nossa sensibilidade auditiva.
O brilho das estrelas e a Lei de Moore:
As escalas logarítmicas brilham intensamente na astronomia, onde auxiliam na quantificação da luminosidade dos objetos celestes. O sistema de magnitude, enraizado em princípios logarítmicos, permite aos astrônomos classificar estrelas com base no seu brilho. Da mesma forma, a Lei de Moore, uma observação renomada no domínio da computação, reflete o crescimento exponencial no número de transistores em circuitos integrados – um conceito firmemente fundamentado na progressão logarítmica.
Equilíbrio do pH:
Em química, o equilíbrio do pH é uma métrica para avaliar a concentração de íons de hidrogênio em uma solução. Ele é avaliado em uma escala logarítmica que vai de 0 a 14. Cada mudança de unidade na escala de pH significa uma alteração dez vezes maior na concentração de íons de hidrogênio – um aspecto fundamental para compreender a acidez ou alcalinidade de uma substância.
Desbloqueando o potencial das escalas logarítmicas: quando e onde aplicá-las
As escalas logarítmicas, um recurso formidável na visualização de dados, ganham destaque quando confrontadas com conjuntos de dados caracterizados por grandes disparidades de magnitude. Estas escalas oferecem vantagens distintas, especialmente ao visualizar variações percentuais substanciais ou representar dados que aderem a padrões de crescimento exponencial. Vamos nos aprofundar nos cenários e nos domínios em que as escalas logarítmicas devem ser estrategicamente empregadas:
Navegar em magnitudes de dados díspares:
As escalas logarítmicas brilham em situações em que os valores dos dados se espalham por múltiplas ordens de magnitude. Eles se destacam ao tratar dados que não estão em conformidade com uma distribuição uniforme – casos em que um punhado de pontos de dados excede significativamente ou fica muito aquém da maioria. Imagine, por exemplo, um gráfico que ilustra os lucros de 100 filiais de lojas de departamentos. Se duas ou três filiais superarem notavelmente as restantes, a adoção de uma escala linear pode esmagar os dados das outras 98 filiais, encobrindo assim tendências identificáveis. Aí surgem as escalas logarítmicas, resolvendo esse dilema com elegância e permitindo uma representação mais equitativa do conjunto de dados completo.
Visualizar mudanças percentuais e fatores multiplicativos:
As escalas logarítmicas demonstram sua habilidade em capturar flutuações percentuais e fatores multiplicativos. Considere o caso de uma loja que começa vendendo um produto no primeiro ano, duplicando suas vendas a cada ano subsequente. Um gráfico linear convencional pode representar uma fase prolongada de crescimento gradual seguida por um aumento repentino. No entanto, uma escala logarítmica pinta um quadro mais autêntico, retratando uma duplicação consistente a cada ano como uma linha reta do canto inferior esquerdo ao canto superior direito. Esta representação reflete com precisão a natureza exponencial dos dados, tornando-a uma escolha privilegiada para tais cenários.
Campos que adotam escalas logarítmicas:
Vários campos aproveitam rotineiramente os recursos das escalas logarítmicas para enfrentar vários desafios. Aqui estão alguns exemplos dignos de nota:
- Ciências atuariais: os atuários recorrem a escalas logarítmicas para calcular métricas de seguros, avaliar custos e examinar riscos, especialmente quando confrontados com extensos conjuntos de dados.
- Medicina: Os médicos recorrem frequentemente a escalas logarítmicas na medicina nuclear e interna, especialmente para medições relacionadas com concentrações de pH, decaimento radioativo, dinâmica de saúde e proliferação bacteriana.
- Arqueologia: Os arqueólogos empregam funções logarítmicas para determinar a idade de artefatos, plantas e fibras antigas, analisando isótopos de carbono.
- Matemática: As escalas logarítmicas servem como ferramentas fundamentais em estatística e análise, especialmente quando se trata de problemas baseados em equações exponenciais.
- Finanças: Os especialistas financeiros aproveitam incrementos logarítmicos para transmitir as taxas de juros de forma eficaz, destacando o crescimento dos investimentos ou elucidando a situação financeira de indivíduos ou grupos.
Selecionando os gráficos apropriados para escalas logarítmicas
Escolher o tipo de gráfico certo para complementar as escalas logarítmicas é fundamental para garantir uma visualização eficaz dos dados. Nem todos os tipos de gráficos se harmonizam facilmente com escalas logarítmicas, principalmente porque avaliações precisas de comprimento tornam-se essenciais. No entanto, várias opções de gráficos se alinham perfeitamente com escalas logarítmicas, cada uma trazendo pontos fortes únicos. Vamos nos aprofundar nos tipos de gráficos que sinergizam suavemente com escalas logarítmicas e destacar suas vantagens distintas:
Gráficos de pontos:
Os gráficos de pontos oferecem uma alternativa atraente aos gráficos de barras tradicionais usados em escalas logarítmicas. Eles possuem uma vantagem significativa em termos de clareza. Em contraste com os gráficos de barras, onde o comprimento das barras serve como uma representação visual dos valores, os gráficos de pontos empregam pontos discretos que não transmitem inerentemente um valor específico. Esta característica harmoniza-se perfeitamente com os princípios que sustentam as escalas logarítmicas. Os gráficos de pontos podem ser implantados nas orientações horizontal e vertical, o que traz versatilidade na representação de dados. A sua aparência organizada facilita muito a representação precisa dos valores, especialmente quando aplicado a escalas logarítmicas.
Gráficos de linhas:
Os gráficos de linhas surgem como uma escolha confiável para visualizar dados em escalas logarítmicas. A sua capacidade inata de ilustrar tendências e padrões torna-os excepcionalmente adequados para gráficos logarítmicos. As linhas suaves e contínuas apresentadas nestes gráficos são excelentes para revelar o crescimento ou declínio exponencial inerente aos dados logarítmicos. Seja monitorando o desempenho financeiro, examinando fenômenos científicos ou lidando com qualquer conjunto de dados caracterizado por atributos exponenciais, os gráficos de linhas fornecem um meio perspicaz e intuitivo de transmitir informações.
Gráficos especializados para ações:
Gráficos especializados para ações são indispensáveis para indivíduos envolvidos em análises financeiras e empreendimentos de negociação de ações. Eles abrangem gráficos de velas, gráficos Kagi, gráficos Renko e outros. Esses gráficos transcendem a mera representação de pontos de dados; eles fornecem insights abrangentes sobre preços de compra e venda, tendências de preços e sentimento de mercado em torno de ações específicas. Embora não sejam projetados exclusivamente para escalas logarítmicas, eles complementam perfeitamente os gráficos de escala logarítmica, especialmente ao dissecar ações e tendências de ações.
Prós e contras dos gráficos logarítmicos: equilibrando insights e limitações
Os gráficos logarítmicos são recursos inestimáveis na visualização de dados, oferecendo vantagens e limitações distintas que merecem consideração cuidadosa ao optar por eles como método de representação. Abaixo, investigamos os pontos fortes e fracos dos gráficos logarítmicos para obter uma compreensão abrangente de sua utilidade.
Vantagens dos gráficos logarítmicos:
Visibilidade aprimorada de tendências:
Os gráficos logarítmicos são excelentes para identificar e enfatizar tendências. Ao refletirem fielmente os dados subjacentes, simplificam a identificação de tendências com notável precisão. Quando as linhas de tendências são sobrepostas a um gráfico logarítmico, a disparidade entre ele e um gráfico linear torna-se evidente. Os gráficos logarítmicos geralmente fornecem uma representação mais fiel das tendências, especialmente quando se trata de conjuntos de dados de crescimento ou declínio exponencial.
Perspectiva de longo prazo:
As perspectivas de longo prazo normalmente abrangem uma duração prolongada, marcada por flutuações e crescimento substanciais. As escalas logarítmicas capturam habilmente essas trajetórias dinâmicas. Numa escala linear, estes períodos prolongados de transformação podem parecer comprimidos e sem clareza, enquanto as escalas logarítmicas acomodam graciosamente as mudanças radicais frequentemente observadas em dados de longo prazo.
Acomodação de uma ampla faixa de dados:
As escalas logarítmicas superam o desafio colocado pelos valores discrepantes de dados. Os valores discrepantes podem exercer pressão sobre a maioria dos pontos de dados quando plotados em uma escala linear, tornando-os potencialmente menos discerníveis. As escalas logarítmicas abordam esse problema de maneira eficaz, garantindo que os pontos de dados individuais mantenham a visibilidade e não sejam ofuscados por valores extremos. Isso os torna uma excelente escolha ao lidar com conjuntos de dados caracterizados por intervalos variados.
Desvantagens dos gráficos logarítmicos:
Ausência de zero absoluto:
Uma limitação digna de nota das escalas logarítmicas é a ausência de um ponto zero absoluto. Dado que um valor não pode ser elevado à potência de zero em termos logarítmicos, os gráficos logarítmicos não podem começar do zero. Embora esta limitação possa não apresentar problemas para certos tipos de dados, ela exige uma consideração cuidadosa por parte dos criadores de gráficos. A ausência de um ponto zero pode confundir os espectadores não versados em escalas logarítmicas.
Interpretação complexa:
Os gráficos logarítmicos não são adaptados para fornecer valores numéricos explícitos, mas para enfatizar tendências. Este aspecto pode torná-los difíceis de interpretar para indivíduos que esperam números precisos. Os visualizadores devem compreender a natureza logarítmica da escala para analisar com eficácia os gráficos logarítmicos, o que pode exigir explicações complementares e rotulagem no próprio gráfico.
Incompatibilidade com valores negativos:
Os gráficos logarítmicos são menos adequados para representar números positivos e negativos na mesma escala. As funções logarítmicas carecem de soluções para valores negativos, o que limita a sua aplicabilidade em cenários onde é necessária a visualização de valores positivos e negativos.
Os gráficos logarítmicos surgem como recursos potentes na visualização de dados, oferecendo vantagens distintas que se tornam especialmente valiosas ao lidar com conjuntos de dados caracterizados por variações substanciais de magnitude ou tendências de crescimento exponencial. A sua notável capacidade de ampliar a visibilidade das tendências, facilitar a análise de perspectivas a longo prazo e lançar luz sobre a influência de valores discrepantes torna-os ferramentas indispensáveis em diversos domínios, desde complexidades financeiras até as fronteiras da investigação científica.
No entanto, é imperativo reconhecer as limitações inerentes aos gráficos logarítmicos. Elas incluem a ausência de um ponto zero absoluto, a compreensão necessária da sua natureza logarítmica pelos observadores e a sua inadequação para visualizar valores negativos. Para aproveitar totalmente o potencial incorporado nos gráficos logarítmicos, é fundamental considerar meticulosamente as características inerentes dos dados e os objetivos precisos do esforço de visualização.
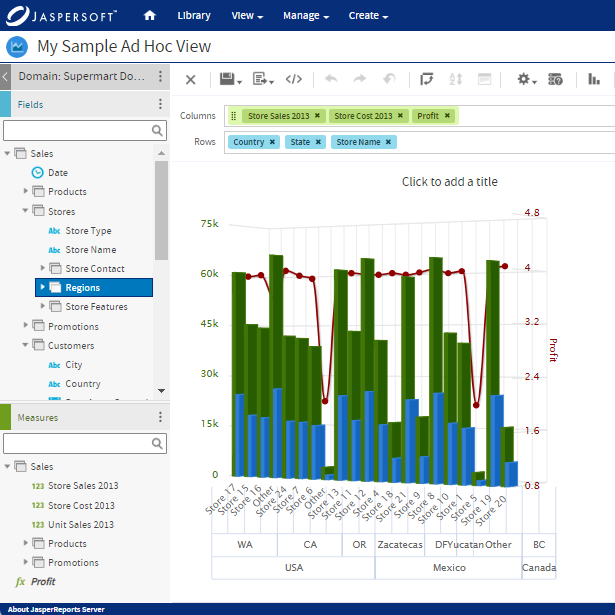
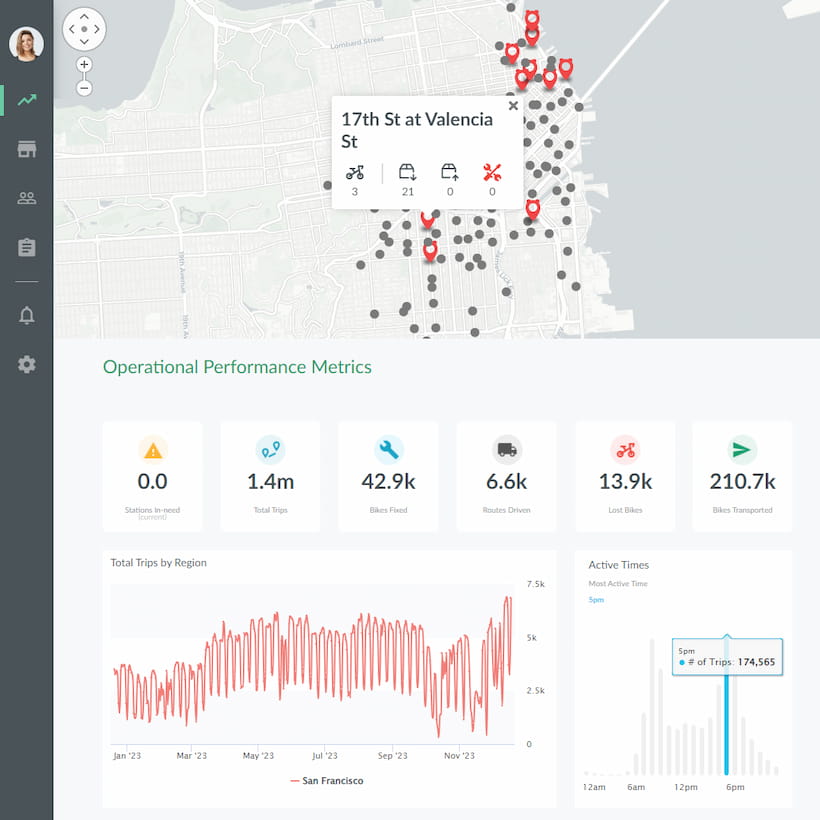
Gráficos logarítmicos com Jaspersoft
Recursos relacionados
Jaspersoft in Action: Embedded BI Demo
See everything Jaspersoft has to offer – from creating beautiful data visualizations and dashboards to embedding them into your application.
Creating Addictive Dashboards
Learn how to build dashboards that your users will love. Turn your data into interactive, visually engaging metrics that can be embedded into your web application.
