¿Qué es un gráfico logarítmico?
Un gráfico logarítmico es una representación gráfica que emplea una escala logarítmica, que se diferencia de la escala lineal convencional utilizada en la mayoría de los gráficos, donde los valores se espacian uniformemente creando intervalos variables entre valores.

A diferencia de la escala lineal estándar que se ve comúnmente en la mayoría de los gráficos tradicionales, un gráfico logarítmico emplea una escala logarítmica. A diferencia de las escalas lineales, que espacian los valores uniformemente, las escalas logarítmicas crean espacios variables entre los valores, lo que resulta en ventajas notables. Este enfoque logarítmico es ventajoso cuando se trata de conjuntos de datos que abarcan una amplia gama de valores. Permite una forma más ágil y eficiente en cuanto a espacio de presentar información numérica.
Los logaritmos introducen un toque de no linealidad en el mundo de la representación matemática. Para comprender este concepto, considere los números 10 y 20 en comparación con 80 y 90. En la escala logarítmica, los intervalos entre estos valores no son uniformes; en cambio, aparecen intervalos uniformes entre números como 10 y 100 o 60 y 600, ya que representan un aumento constante del valor del 100 por ciento.
En esencia, los logaritmos proporcionan un método alternativo para expresar ecuaciones exponenciales. Este enfoque permite la separación del exponente en un lado de una ecuación. Por ejemplo, la ecuación 42 = 16 se puede transformar en "log en base 4 de 16 es igual a 2", aunque a menudo se enuncia como "log en base 4 de 16 es 2". En este caso, el logaritmo simbolizado como log, emplea una base de 4 y es igual a 2.
En la ecuación y = log base b (x), y simboliza el exponente o potencia necesaria para elevar b para lograr x. Esta representación logarítmica es fundamental en numerosas aplicaciones matemáticas y científicas, proporcionando una perspectiva distintiva sobre la conexión entre los números y sus características exponenciales.
¿Cómo funciona la escala logarítmica?
Establecer una escala es una tarea sencilla en el dominio de las funciones lineales. Se pueden emplear incrementos de números enteros donde cada paso representa una unidad de medida idéntica e invariable. Este enfoque se puede comparar con marcar una regla, donde el espacio entre cada marca sigue siendo el mismo. Sin embargo, cuando nos centramos en funciones logarítmicas, la escala asume un carácter distinto estrechamente ligado a los exponentes mediante los cuales se eleva un valor.
Para verlo en profundidad, contemplemos un gráfico lineal caracterizado por una escala que aumenta en uno. En este escenario, cada paso hacia adelante o hacia atrás en el gráfico corresponde a un cambio de una unidad. Ahora, comparemos esto con un gráfico logarítmico, en el que la escala se basa en las potencias de un número específico, a menudo tomado como 10.
Pongamos como ejemplo una situación hipotética en la que el proceso de ventas de una empresa comenzó con una única venta en 1999. Sorprendentemente, esta cifra se duplicó cada año posterior hasta el año 2011. Si empleamos una escala lineal en este contexto, representará las cifras de ventas brutas y absolutas registradas durante estos años. Tal representación ilustraría un aumento gradual, pasando de una venta única en 1999 a una cifra de dos dígitos en 2000, y así sucesivamente.
Sin embargo, adoptar una escala logarítmica presentaría una perspectiva completamente distinta. En lugar de resaltar los valores numéricos brutos, acentuaría el ritmo de cambio en las ventas a lo largo de este período. En este caso, subrayaría que las cifras de ventas se duplicaron anualmente. Esta representación logarítmica nos proporciona un punto de vista único que facilita el discernimiento de patrones de crecimiento exponencial con una claridad excepcional.
Profundización en los fundamentos de las escalas logarítmicas
Las escalas logarítmicas representan un potente instrumento en la visualización de datos, ya que ofrecen un medio conciso y esclarecedor para transmitir grandes volúmenes de información. Su aplicabilidad abarca diversos campos, que confieren ventajas a los analistas, investigadores y tomadores de decisiones de diversas organizaciones. Es imperativo tener una comprensión firme de los fundamentos de las escalas logarítmicas para aprovechar su potencial de manera efectiva. A continuación, presentamos varias ideas clave a tener en cuenta:
Gráficos semilogarítmicos:
Un gráfico es "semilogarítmico" cuando solo uno de sus ejes adopta una escala logarítmica. Este enfoque permite una representación versátil de los datos, en la que un eje se adhiere a la progresión lineal habitual mientras que el otro se adhiere al principio logarítmico. Estos gráficos resultan particularmente ventajosos cuando se enfrentan a conjuntos de datos caracterizados por un crecimiento o disminución exponencial a lo largo de un eje mientras mantienen una trayectoria lineal a lo largo del otro.
Representación logarítmica:
Por el contrario, la representación logarítmica emplea escalas logarítmicas tanto para el eje x como para el eje y. Este tratamiento logarítmico dual resulta de gran valor cuando se examinan relaciones intrincadas entre variables que abarcan múltiples órdenes de magnitud. Puede revelar patrones y correlaciones intrincados que podrían permanecer ocultos cuando se utilizan escalas lineales.
Restricciones de escalas logarítmicas:
Si bien las escalas logarítmicas ofrecen diversos beneficios, presentan ciertas limitaciones. Una limitación fundamental radica en su incapacidad para representar números negativos o cero. Esta limitación emana del principio matemático central de que es inherentemente inalcanzable derivar estos valores elevando un número base a cualquier exponente. Las escalas logarítmicas están diseñadas exclusivamente para valores positivos, lo que las hace menos adecuadas para conjuntos de datos que abarcan fenómenos basados en la negatividad o el cero.
El valor logarítmico mínimo:
Dentro de una escala logarítmica, el cero aparece como el valor absoluto más bajo imaginable. En el ámbito de los logaritmos, esto equivale a un resultado de uno, ya que cualquier entidad numérica elevada a la potencia de cero invariablemente da como resultado uno. Comprender esta faceta fundamental de las escalas logarítmicas es importante al interpretar datos estructurados en este formato particular.
Aplicaciones en diversos tipos de gráficos:
La adaptabilidad de las escalas logarítmicas se extiende a muchos tipos de gráficos, desde gráficos de líneas y gráficos de barras hasta gráficos circulares y diagramas de dispersión. Esta versatilidad brinda a los analistas la capacidad de visualizar y transmitir datos en diversos contextos, facilitando así una comprensión más profunda de tendencias y fenómenos complejos.
La importancia de integrar escalas logarítmicas en la visualización de datos
La incorporación de escalas logarítmicas en la representación de datos va más allá de la mera preferencia; tiene un peso significativo en nuestra capacidad de transmitir información compleja de manera efectiva. Las escalas logarítmicas emergen como herramientas indispensables para abordar una variedad de desafíos visuales, especialmente en el manejo de conjuntos de datos extensos, en particular aquellos plagados de fluctuaciones sustanciales de valor. Garantizan que las ideas críticas sean fácilmente discernibles para la audiencia.
Consideremos un escenario donde los datos se presentan a través de un gráfico de barras. Este conjunto de datos comprende numerosos valores, la mayoría dentro de un rango relativamente estrecho, mientras que unos pocos exhiben valores significativamente elevados. Cuando se representan en una escala lineal, estas disparidades de magnitud pueden crear obstáculos formidables para los espectadores que se esfuerzan por extraer información del gráfico.
Las escalas logarítmicas solucionan este dilema remodelando la representación visual de los datos, y de ahí su importancia.
Igualación del impacto visual:
Las escalas logarítmicas comprimen valores más grandes y expanden los más pequeños. Este efecto de compresión y expansión nivela el campo visual para los puntos de datos en el gráfico, facilitando la diferenciación entre valores de diferentes magnitudes. En consecuencia, los espectadores pueden captar todo el espectro de datos sin la distracción de valores atípicos desproporcionadamente prominentes.
Claridad en medio de la complejidad:
Las escalas logarítmicas en conjuntos de datos marcados por grandes variaciones aportan estructura a lo que de otro modo podría ser caótico. Organizan la información de una manera que mantiene la integridad de cada punto de datos y al mismo tiempo frena el predominio de unos pocos valores atípicos excepcionales. Esta organización es vital en la investigación científica, el análisis financiero y otros ámbitos donde la precisión y la sutileza son primordiales.
Facilitan la toma de decisiones informada:
La adopción de escalas logarítmicas fomenta la toma de decisiones informadas. Al eliminar las distorsiones causadas por los valores extremos, los responsables de la toma de decisiones pueden formular juicios sólidos basados en una representación de datos más precisa. Las escalas logarítmicas mejoran la probabilidad de tomar decisiones acertadas, ya sea evaluando tendencias del mercado, examinando fenómenos científicos o cualquier otro campo que dependa de conocimientos basados en datos.
Elevan la comunicación de los datos:
Las escalas logarítmicas amplifican la destreza comunicativa de diagramas y gráficos. Permiten a los analistas e investigadores de datos transmitir información compleja de manera sucinta y comprensible. Esto resulta particularmente ventajoso cuando se presentan hallazgos a audiencias diversas con distintos niveles de conocimiento numérico.
El potencial de la fórmula logarítmica
Aprovechar el potencial que reside en las escalas logarítmicas va más allá de un mero ejercicio numérico; es una habilidad fundamental que le permite navegar fácilmente a través de extensos conjuntos de datos y descifrar conexiones exponenciales complejas. Para emplear hábilmente la fórmula logarítmica (y = log₁₀(x)) y desentrañar las sutilezas entretejidas en las escalas logarítmicas, siga estos pasos estratégicos:
Sustitución de la variable y:
Los logaritmos, en esencia, ofrecen una vía simplificada para desentrañar funciones exponenciales complejas. Comience por identificar la base, a menudo 10, y discierna el papel que desempeña la variable y en su contexto específico. Una vez comprenda esto, embárquese en el viaje para calcular la función y desvelar los secretos de la variable x. Por ejemplo, imagine que tiene la tarea de graficar una función logarítmica y obtiene un valor de y de 1500. Implemente este valor en la fórmula como se ilustra a continuación:
1.500 = log₁₀(x)
Cálculo de la función logarítmica:
Para desenterrar la elusiva variable x, el siguiente paso consiste en resolver la función logarítmica utilizando destreza algebraica. Reflexionando sobre nuestro ejemplo anterior con un valor de y de 1500, cambie su perspectiva hacia una función exponencial y ejecute el cálculo de la siguiente manera:
10^x = 1.500
Al resolver el valor de x, tendrá la clave para definir la escala de su gráfico.
Determinación de la variable x:
Una vez que se han sentado las bases meticulosamente, ha llegado el momento de deducir la variable x. Esta variable esencialmente dicta el incremento por el cual cada paso en su escala logarítmica avanza o retrocede. Volviendo a nuestro ejemplo anterior, al resolver la ecuación 10^x = 1500 se obtiene un valor de x de aproximadamente 3,18. Esto implica que por cada cambio incremental en el valor de y, el valor de x correspondiente aumenta diez veces con respecto al valor de x anterior. Para ilustrarlo mejor, si el valor de y supera 1501, el valor de x ascenderá a aproximadamente 31,76.
Este proceso en tres pasos le permite utilizar hábilmente la fórmula logarítmica, decodificar relaciones exponenciales intrincadas, construir escalas significativas y recorrer con confianza conjuntos de datos intrincados. Ya sea que sus esfuerzos giren en torno a la exploración científica, la modelización financiera o cualquier disciplina que exija precisión y conocimiento, el dominio de la fórmula logarítmica le proporciona una herramienta formidable para descifrar la dinámica de los datos numéricos.
La importancia de adoptar escalas logarítmicas
Las escalas logarítmicas, una herramienta fundamental en la representación de datos, proporcionan un medio distintivo para dar cuenta de las intrincadas variaciones presentes en una amplia gama de fenómenos. He aquí por qué las personas recurren a escalas logarítmicas para comprender mejor las complejidades del mundo que nos rodea:
Sensibilidad al cambio:
Nuestro mundo rara vez experimenta cambios en incrementos uniformes. Tomemos como ejemplo la temperatura. Piense en la diferencia entre 20 y 25 grados; apenas se nota. Por el contrario, la brecha entre 40 y 45 grados es palpable. Aunque estos cambios de temperatura pueden parecer lineales cuando se los coloca en una escala, nuestra percepción de ellos está lejos de ser lineal. Las escalas logarítmicas nos permiten capturar con precisión estas diferencias discernibles comprimiendo valores más grandes y expandiendo los más pequeños. Proporcionan una representación de datos que se alinea con nuestro sentido innato de cambio, haciéndolo más identificable e intuitivo.
La escala de Richter:
La escala de Richter, una herramienta empleada para medir la magnitud de los terremotos, es un ejemplo clásico de escalas logarítmicas. Quienes tienen experiencia en eventos sísmicos comprenden que distinguir entre un terremoto de magnitud 2,5 y 3,5 es un desafío, mientras que una diferencia de una unidad entre 5,5 y 6,5 es evidente. La escala de Richter revela la verdadera naturaleza de la liberación de energía sísmica, donde cada incremento de un número entero significa no una amplificación lineal sino diez veces mayor en amplitud. Esta amplificación del cambio en niveles superiores subraya la imprescindibilidad de las escalas logarítmicas para comprender la actividad sísmica.
Decibelios:
Las escalas logarítmicas ocupan una posición central en el ámbito del sonido. Las mediciones de decibelios, utilizadas frecuentemente en acústica, ingeniería de audio y telecomunicaciones, expresan la intensidad del sonido y las relaciones de potencia de forma logarítmica. Este enfoque nos permite navegar por el amplio rango de la percepción auditiva humana, abarcando el espectro desde susurros apenas audibles hasta sonidos atronadores, y reflejando nuestra sensibilidad auditiva.
Brillo de las estrellas y ley de Moore:
Las escalas logarítmicas brillan intensamente en astronomía, donde ayudan a cuantificar la luminosidad de los objetos celestes. El sistema de magnitud, basado en principios logarítmicos, permite a los astrónomos clasificar las estrellas en función de su brillo. De manera similar, la Ley de Moore, una observación reconocida en el ámbito de la computación, refleja un crecimiento exponencial en el número de transistores en los circuitos integrados, un concepto firmemente basado en la progresión logarítmica.
Equilibrio del pH:
En química, el equilibrio del pH es una métrica para evaluar la concentración de iones de hidrógeno en una solución. Se evalúa en una escala logarítmica que va de 0 a 14. Cada cambio de unidad en la escala de pH significa una alteración diez veces mayor en la concentración de iones de hidrógeno, un aspecto fundamental para comprender la acidez o alcalinidad de una sustancia.
Desentrañando el potencial de las escalas logarítmicas: cuándo y dónde aplicarlas
Las escalas logarítmicas, un activo formidable en la visualización de datos, pasan a ser el centro de atención cuando se enfrenta a conjuntos de datos caracterizados por grandes disparidades en magnitud. Estas escalas ofrecen ventajas distintivas, particularmente cuando se visualizan variaciones porcentuales sustanciales o se representan datos que se adhieren a patrones de crecimiento exponencial. Profundicemos en los escenarios y los dominios en los que se deberían emplear estratégicamente las escalas logarítmicas:
Navegación por magnitudes de datos dispares:
Las escalas logarítmicas brillan en situaciones en las que los valores de los datos se extienden en múltiples órdenes de magnitud. Pasan a primer plano cuando se abordan datos que no se ajustan a una distribución uniforme: casos en los que un puñado de puntos de datos superan significativamente o están muy por debajo de la mayoría. Imagine, por ejemplo, un gráfico que ilustra las ganancias de 100 sucursales de grandes almacenes. Si dos o tres sucursales superan notablemente al resto, la adopción de una escala lineal puede aplastar los datos de las 98 sucursales restantes, oscureciendo así las tendencias discernibles. Al introducir escalas logarítmicas, resuelve elegantemente este dilema y logra una representación más equitativa del conjunto de datos completo.
Visualización de cambios porcentuales y factores multiplicativos:
Las escalas logarítmicas demuestran su destreza para capturar fluctuaciones porcentuales y factores multiplicativos. Pongamos el caso de una tienda que comienza vendiendo un producto durante el primer año y va duplicando sus ventas en los años posteriores. Un gráfico lineal convencional podría representar una fase prolongada de crecimiento gradual seguida de un pico repentino. Sin embargo, una escala logarítmica ofrece una imagen más auténtica, mostrando una duplicación constante cada año como una línea directa desde la esquina inferior izquierda hasta la esquina superior derecha. Esta representación refleja con precisión la naturaleza exponencial de los datos, lo que la convierte en una excelente opción para tales escenarios.
Campos que adoptan escalas logarítmicas:
Numerosos campos aprovechan habitualmente las capacidades de las escalas logarítmicas para abordar diversos desafíos. Aquí hay algunos ejemplos notables:
- Ciencia actuarial: los actuarios se basan en escalas logarítmicas para calcular métricas de seguros, evaluar costes y examinar riesgos, particularmente cuando se enfrentan a conjuntos de datos extensos.
- Medicina: los médicos recurren con frecuencia a escalas logarítmicas en medicina nuclear e interna, especialmente para mediciones relacionadas con concentraciones de pH, desintegración radiactiva, dinámica de salud y proliferación bacteriana.
- Arqueología: los arqueólogos emplean funciones logarítmicas para determinar las edades de artefactos, plantas y fibras antiguas mediante el análisis de isótopos de carbono.
- Matemáticas: las escalas logarítmicas sirven como herramientas fundamentales en estadística y análisis, particularmente cuando se enfrentan problemas basados en ecuaciones exponenciales.
- Finanzas: los expertos financieros aprovechan los incrementos logarítmicos para transmitir las tasas de interés de manera efectiva, destacando el crecimiento de las inversiones o aclarando la situación financiera de individuos o grupos.
Selección de los gráficos apropiados para escalas logarítmicas
Elegir el tipo de gráfico adecuado para complementar las escalas logarítmicas es fundamental para garantizar una visualización de datos eficaz. No todos los tipos de gráficos armonizan fácilmente con las escalas logarítmicas, principalmente porque las evaluaciones precisas de la longitud se vuelven esenciales. Sin embargo, varias opciones de gráficos se alinean perfectamente con escalas logarítmicas y cada una aporta ventajas únicas. Profundicemos en los tipos de gráficos que combinan perfectamente con las escalas logarítmicas y resaltemos sus ventajas distintivas:
Gráficos de puntos:
Los gráficos de puntos ofrecen una alternativa convincente a los gráficos de barras tradicionales que operan en escalas logarítmicas. Poseen una ventaja significativa en términos de claridad. A diferencia de los gráficos de barras, donde la longitud de las barras sirve como una representación visual de los valores, los gráficos de puntos emplean puntos discretos que no transmiten inherentemente un valor específico. Esta característica armoniza perfectamente con los principios que sustentan las escalas logarítmicas. Los gráficos de puntos se pueden orientar tanto en horizontal como en vertical, lo que les confiere versatilidad en la representación de datos. Su apariencia ordenada facilita enormemente la representación precisa de valores, particularmente cuando se aplican a escalas logarítmicas.
Gráficos de líneas:
Los gráficos de líneas surgen como una opción confiable al visualizar datos en escalas logarítmicas. Su capacidad innata para ilustrar tendencias y patrones los hace excepcionalmente adecuados para gráficos logarítmicos. Las líneas suaves y continuas que aparecen en estos gráficos destacan por revelar el crecimiento o la disminución exponencial inherente a los datos logarítmicos. Ya sea monitoreando el rendimiento financiero, examinando fenómenos científicos o manejando cualquier conjunto de datos caracterizado por atributos exponenciales, los gráficos de líneas proporcionan un medio esclarecedor e intuitivo para transmitir información.
Gráficos especializados de acciones y valores:
Los gráficos especializados de acciones y valores resultan indispensables para las personas que se dedican al análisis financiero y las operaciones bursátiles. Estos incluyen los gráficos candlestick, gráficos Kagi y gráficos Renko, entre otros. Estos gráficos trascienden la mera descripción de puntos de datos; proporcionan información detallada sobre los precios de compra y venta, las tendencias de los precios y el sentimiento del mercado en torno a acciones específicas. Aunque no están diseñados exclusivamente para escalas logarítmicas, complementan a la perfección los gráficos de escalas logarítmicas, especialmente cuando analizan acciones y tendencias.
Pros y contras de los gráficos logarítmicos: equilibrio entre información y limitaciones
Los gráficos logarítmicos son activos invaluables en la visualización de datos, ya que ofrecen ventajas y limitaciones distintivas que justifican una cuidadosa consideración al optar por ellos como método de representación. A continuación, profundizamos en las fortalezas y debilidades de los gráficos logarítmicos para obtener una comprensión integral de su utilidad.
Ventajas de los gráficos logarítmicos:
Visibilidad de tendencias mejorada:
Los gráficos logarítmicos destacan por hacer que las tendencias sean más pronunciadas y discernibles. Al reflejar fielmente los datos subyacentes, simplifican la identificación de tendencias con notable precisión. Cuando las líneas de tendencia se superponen en un gráfico logarítmico, la disparidad entre este y un gráfico lineal se vuelve evidente. Los gráficos logarítmicos suelen proporcionar una representación más fiel de las tendencias, especialmente cuando se trata de conjuntos de datos de crecimiento o declive exponencial.
Perspectiva a largo plazo:
Las perspectivas a largo plazo suelen abarcar duraciones prolongadas marcadas por fluctuaciones y crecimiento sustanciales. Las escalas logarítmicas capturan hábilmente estas trayectorias dinámicas. En una escala lineal, estos prolongados períodos de transformación pueden parecer comprimidos y carentes de claridad, mientras que las escalas logarítmicas se adaptan elegantemente a los cambios radicales que a menudo se observan en los datos a largo plazo.
Alojamiento de un amplio rango de datos:
Las escalas logarítmicas superan el desafío que plantean los valores atípicos dentro de los datos. Los valores atípicos pueden ejercer presión sobre la mayoría de los puntos de datos cuando se trazan en una escala lineal, haciéndolos potencialmente menos discernibles. Las escalas logarítmicas abordan eficazmente este problema, garantizando que los puntos de datos individuales mantengan visibilidad y no se vean eclipsados por valores extremos. Esto los convierte en una excelente opción cuando se manejan conjuntos de datos caracterizados por rangos diversos.
Desventajas de los gráficos logarítmicos:
Ausencia de un cero absoluto:
Una limitación notable de las escalas logarítmicas es la ausencia de un punto cero absoluto. Dado que un valor no se puede elevar a la potencia de cero en términos logarítmicos, los gráficos logarítmicos no pueden iniciarse desde cero. Si bien esta limitación puede no presentar problemas para ciertos tipos de datos, requiere una cuidadosa consideración por parte de los creadores de gráficos. La ausencia de un punto cero podría confundir a los espectadores que no estén bien versados en escalas logarítmicas.
Interpretación compleja:
Los gráficos logarítmicos no están diseñados para proporcionar valores numéricos explícitos sino para subrayar tendencias. Este aspecto puede hacer que su interpretación sea difícil para quienes esperan cifras numéricas precisas. Deben comprender la naturaleza logarítmica de la escala para analizar eficazmente los gráficos logarítmicos, lo que puede requerir explicaciones y etiquetas adicionales en el propio gráfico.
Incompatibilidad con valores negativos:
Los gráficos logarítmicos son menos adecuados para representar números positivos y negativos en la misma escala. Las funciones logarítmicas carecen inherentemente de soluciones para valores negativos, lo que limita su aplicabilidad en escenarios donde se requiere la visualización de valores tanto positivos como negativos.
Los gráficos logarítmicos emergen como activos potentes en la visualización de datos, ofreciendo distintas ventajas que se vuelven especialmente valiosas cuando se trata de conjuntos de datos caracterizados por variaciones sustanciales en magnitud o tendencias de crecimiento exponencial. Su notable capacidad para amplificar la visibilidad de las tendencias, facilitar el análisis de perspectivas de largo plazo y arrojar luz sobre la influencia de los valores atípicos los convierte en herramientas indispensables en diversos dominios, que van desde las complejidades de las finanzas hasta las fronteras de la investigación científica.
No obstante, es imperativo reconocer las limitaciones inherentes de los gráficos logarítmicos. Entre ellas se encuentran la ausencia de un punto cero absoluto, la necesaria comprensión por parte del espectador de su naturaleza logarítmica y su inadecuación para visualizar valores negativos. Para aprovechar plenamente el potencial inherente a los gráficos logarítmicos, es fundamental una consideración meticulosa de las características inherentes de los datos y los objetivos precisos del esfuerzo de visualización.
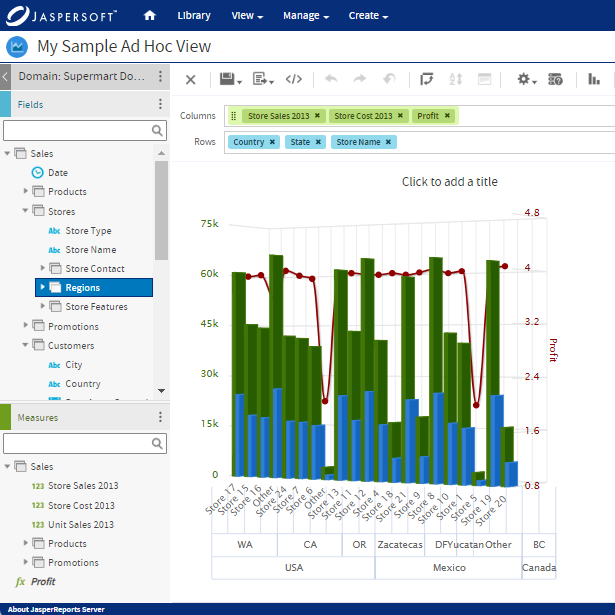
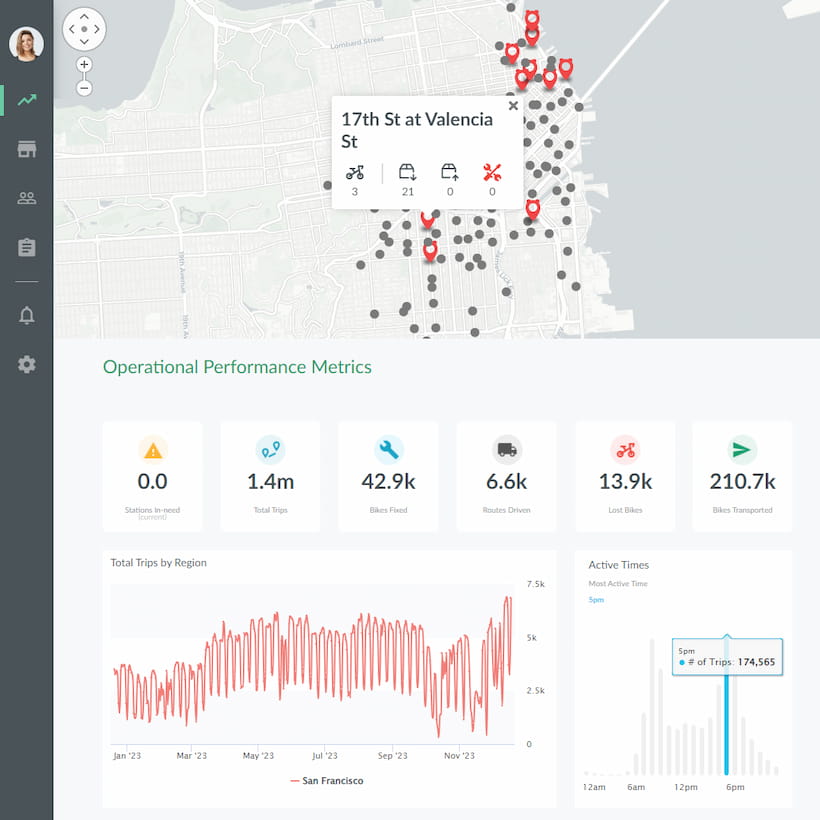
Gráficos logarítmicos con Jaspersoft
Recursos Relacionados
Jaspersoft in Action: Embedded BI Demo
See everything Jaspersoft has to offer – from creating beautiful data visualizations and dashboards to embedding them into your application.
Creating Addictive Dashboards
Learn how to build dashboards that your users will love. Turn your data into interactive, visually engaging metrics that can be embedded into your web application.
