What is a Node Diagram?

A node diagram is a visual representation strategy used for mapping a network of nodes or interconnected entities. Node diagrams play an important role in organizing data in a way that reveals clusters, outliers, important nodes, and relationships in your network or system.

Visualization tools like nodes are important for making sense of vast amounts of data by providing a quick ‘bird’s eye view’ to users. It also helps us understand the data and what it means. To put it briefly, node diagrams consist of a few ‘nodes’ or points that represent the objects in a system, as well as links that represent the relationship between the nodes.

Depending on the application, it makes sense to size the nodes according to a numerical value to represent their importance in the network. Node diagrams have a wide range of applications across numerous disciplines and industries because they simplify decision-making, communication, and analytics.

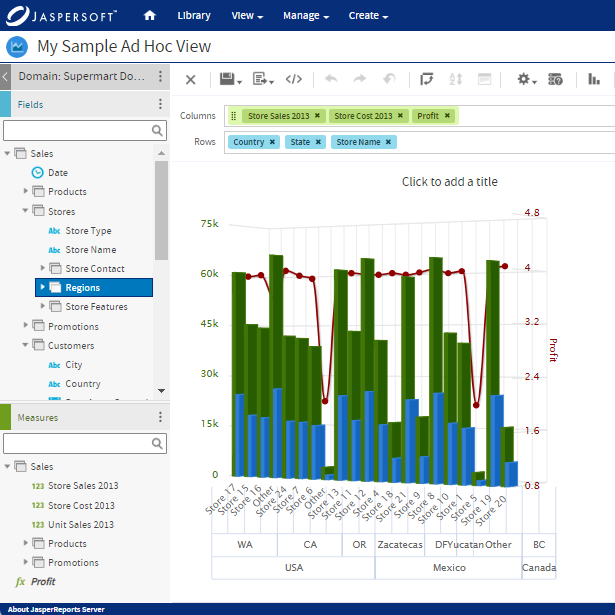
Types of Node Diagrams

A node diagram consists of various points or nodes, also known as edges and vertices. Each type of diagram helps shed light on the relationships or connections between various data points. The use of different types of node diagrams depends on various specific scenarios and applications.

Directed Graphs

A directed graph, also known as a digraph, consists of a finite number of nodes and a finite number of directed arcs that connect the pairs of nodes. Directed graphs do not have a root node, depending on the situation. They have a specific direction where the nodes are one-way, indicating a clear origin point and destination for each edge.

The idea of directed graphs is different from undirected graphs (which will be discussed below), where the edges do not have a clear direction or origin. A directed graph may be used to denote various relationships depending on the context, such as:

Communication

In the context of social media platforms, such as X, nodes can be used to represent specific users, and the directed edges can be used to show how the conversation is flowing from one person to the other.

Dependency

In the context of project management, nodes can be used to represent specific goals, and the directed edges can be used to indicate the order in which the tasks should be completed. For example, the directed graph may help indicate the tasks that must be completed before starting the next one.

Flow

In the context of representing a process, nodes can also be used to denote stages or steps of the process, while the directed edges represent the order in which the steps must be completed.

Hierarchical Relationships

In the case of businesses with a specific organizational structure, nodes could represent positions or employees, and the directed edges may indicate to whom certain employees must report. Thus, a directed graph can be used to indicate a hierarchy that all employees are required to follow.

Directed graphs have various applications in numerous industries, including network analysis, biology, social science, and computer science. They are used for modeling and analyzing systems that have directional dependencies, which makes them an extremely valuable tool for learning about the relationship between various processes.

Undirected Graphs

Simply put, undirected graphs consist of edges that don’t have any direction, hence the name. The edges often indicate a two-way relationship, which essentially means that the edge may move along either direction. Depending on the application, the graph edges may also have weights, which can denote the numerical value (or any other attribute) of the connection between the nodes.

This is in stark contrast with directed graphs (discussed above), where the edges have a one-way relationship from an origin node to a destination node.

An undirected graph consists of the following:

Nodes

The nodes are used to denote an entity or object, also referred to as a vertex. Each vertex could be used for representing any type of data, including locations, people, concepts, objects, or any other type of element, depending on the application.

Edges

Edges are used for connecting pairs of nodes to represent their relationship. An undirected graph, on the other hand, does not have any specific direction. Instead, the graph only indicates the type of relationship that the two nodes have.

Symmetry

Symmetry indicates that the relationship between two nodes flows in both ways. For example, suppose we have two nodes named A and B. The undirected graph shows that the connection flows from A to B and from B to A. This symmetry is a unique characteristic trait of undirected graphs.

Applications of Undirected Graphs

Undirected graphs can be used to represent various applications, including the ones discussed below.

Social Networks

In social media platforms, nodes can be used to represent individuals, and undirected edges to show a relationship. For example, if person A is in a relationship with person B, then person B is also in a relationship with person A.

Spatial Relationships

Nodes could be used for representing locations in geographical applications, and the undirected could be used for reporting connections between the locations.

Collaborative Networks

Collaborative networks may be used in academic applications to represent researchers and collaborators. The undirected edges may be used for signifying collaborations between the researchers and collaborators.

Solving Puzzles

Nodes can be used for representing positions in puzzles such as mazes or for diagnosing network connectivity problems, while the undirected edges may indicate the valid paths between the various positions.

To summarize, undirected graphs simplify relationships where the specific flow of direction is not important. Like directed graphs, undirected graphs have applications in various areas, including biology, social sciences, mathematics, and computer science. In short, any application that requires the analysis of symmetrical patterns or relationships can be represented with a node diagram.

Weighted Graphs

Weighted graphs are graphs in which each node has a numerical weight to indicate its importance in the data set. Most numbers in the graphs are assumed to be positive. Weighted graphs are often used for modeling probabilistic relationships between various nodes.

For example, in a social network, the weight could represent the probability of a connection between two individuals rather than a symmetric relationship such as ‘friend’ or ‘not friend.’

A weighted graph often consists of the following:

Nodes

Like most graphs, the nodes in a weighted graph also represent specific entities to indicate their relationship with one another.

Edges

Like most node diagrams, the edges are used for connecting various pairs to indicate their relationship. The difference, however, boils down to the fact that each edge also has a numerical value, usually a weight value.

Weights

Weights are often assigned to edges to indicate various types of information depending on the application. For example, in the context of transportation, the weights could be used to indicate the distance between locations (nodes). In social media platforms, weights could be used to represent the strength of the relationship between nodes (users).

May be Directed or Undirected

Another feature of weighted graphs is that they may be directed or undirected. This means that the edges may or may not have a direction, depending on whether the relationship is one-way or bidirectional.

Applications of Weighted Graph

Weighted graphs can be used for representing relationships in various fields, such as:

Financial Networks

Financial networks may use weights to represent the value of each transaction or how closely linked each financial relationship may be.

Transportation Networks

In a transportation system, weighted graphs may be used for modeling distances or travel times between each node, which can then be used for calculating the most optimized route.

Graph Clustering

Weighted graphs may be used in data analytics to create a cluster of related entities based on how closely linked they are in terms of their weight.

Project Management

In the context of project management, weighted graphs could be used to represent the duration of each task and the requirements for completing various tasks.

In short, weighted graphs are used for solving problems such as finding the most optimal path or route. The goal is usually to minimize the resources involved in completing a task, such as (distance, cost, or time). Weighted graphs are often used in algorithms such as Kruskal’s algorithm to manipulate weighted graphs for various contexts.

Multigraphs

Multigraphs are graphs that have more than one edge between a pair of nodes. Furthermore, these edges often have more than one endpoint. By contrast with simpler node diagrams, where there is often only one edge between two nodes, multigraphs allow the same node to have multiple edges.

A multigraph consists of the following:

Nodes

Nodes, also referred to as vertices, represent individual points or entities in the graph.

Edges

Edges can be used for representing relationships between various nodes. However, a multigraph allows the same pair of nodes to have multiple edges. It is also worth noting that each edge can have various features denoting different pieces of information, such as weights and labels.

Parallel Edges

Another important feature of multigraphs is that they allow the existence of parallel edges, which means that multiple edges lead to the same pair of nodes. With that said, each edge has its own unique properties that make it distinct from the others.

Applications of Multigraphs

Multigraphs can be used in various applications where the same entities have multiple relationships. Below are a few examples:

Transportation Systems

Multigraphs are particularly useful in transportation networks because they can be used for modeling various transportation routes, making it possible to calculate multiple routes between the same routes. This way, if it isn’t possible to use one route, the driver always has access to an alternative route that also minimizes their use of resources (fuel in this case).

Communication Networks

Multigraphs can be used for representing multiple communication channels between nodes.

Electrical Circuits

Multigraphs are also useful in designing electrical circuits because they can indicate multiple pathways for current.

Social Media Platforms

Multigraphs can also depict various types of relationships or interactions between various users on a social media platform.

Collaborative Networks

Multigraphs are very useful in the context of a professional collaboration network because they can represent multiple collaborative efforts between the same network of collaborators.

In short, multigraphs make it possible to design more complicated relationships that may not be possible with directed or undirected graphs. With that said, they are also much more complex in terms of analysis and visualization. Algorithms that are used for designing multigraphs must also consider the presence of multiple edges between each node and make suitable adaptations.

Depending on the application, multigraphs may be converted into simpler structures such as simple graphs.

How to Create Node Diagrams

There are several steps involved in creating a node diagram. These will be discussed below:

Collecting Data

The most important precursor to designing a node diagram is the collection of data. This may be done through data mining, surveys, and other methods.

Defining Nodes and Edges

Nodes and edges must be labeled according to the data that has been collected.

Visualization Tools

Find a suitable solution tool such as Jaspersoft that can be used to best represent the data available.

Layout

Make sure that the nodes and edges are arranged in a manner that is easy to understand. Various factors should be considered, such as color, node size, and edge thickness. Moreover, the visualization tools must also allow users to apply filters and perform analysis easily.

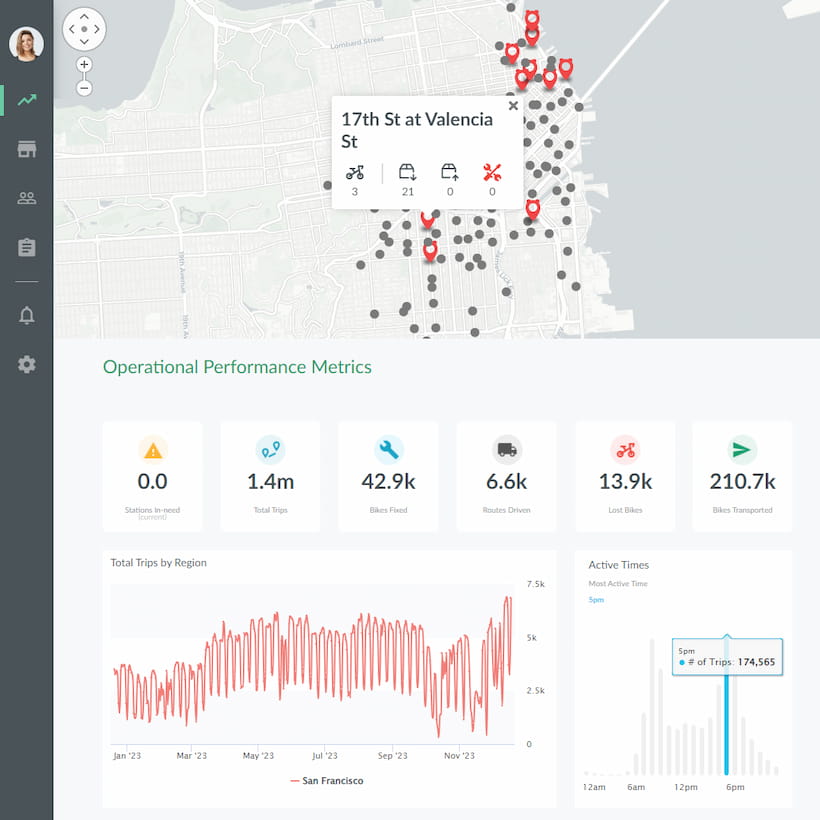
Benefits of Node Diagrams

Node diagrams make it possible to render complex information in a simple manner for users. They utilize various types of visualization techniques discussed earlier to analyze a vast amount of data. This makes it easier for users to make decisions instead of having to go through massive numbers of reports or tables full of raw variables.

Ultimately, node diagrams are used for representing information in a succinct manner so that individuals may be able to make the most optimal and timely decisions. Let’s take a look at some of the main advantages of using node diagrams.

Superior Business Decision

Node diagrams make it possible to effortlessly create intuitive visualizations. As such, individuals may be able to quickly analyze complex data sets on their dashboards.

It helps them find key insights quickly and easily. Node diagrams simplify the process of representing complicated data in a format that is easily understandable for everyone. People tend to understand visual things quicker than reports and tables.

By visually representing the information on a node diagram, it is possible to make complicated information easily understandable for everyone.

As a result, node diagrams enhance communication and collaboration in the decision-making process. Also, it may significantly reduce the risk of error-making when analyzing data. As such, individuals can make superior business decisions and grow their business.

Identifying Trends

A key feature of node diagrams is that they enable effortless analysis of trends. They help users quickly analyze historical and current events and also make it easier to predict future events, such as the growth or decline of potential sales in the future. This also applies to revenue and other important metrics relevant to businesses and organizations.

The human brain is more effective at recognizing and remembering images and visual information. These node diagrams can be used to help teams see and identify insights they may have otherwise missed, create actionable plans, and ultimately boost their bottom line.

Identifying Correlation Between Different Data Points

Correlation is one of the most important applications of node diagrams. They help you discover relationships between independent variables through the use of nodes and edges.

In the context of business intelligence, it is extremely important to find the correlation between market performance and various business units. Node diagrams can help you gain an edge over your competition, track the relationship between your business performance and various operations, and come up with strategic designs to not only grow your company but also beat your competition.

Analysis of Customer

Node diagrams can be used to learn more about customers based on how they interact with your products. With node diagrams, you can more easily gain insights into what your consumers or potential clients are thinking about your brand. You can also learn how your business operations are performing as a whole.

As such, it lets you dig deep into the minds of your potential clients, understand how to sell more products or services to them effectively, and utilize analytics to create superior business strategies.

Increase Your Productivity and Sales

Node diagrams help you visualize data to produce real results. The time you save in creating up-to-date reports means that you can improve your processes across all your business units. Organizations that use node diagrams are more likely to learn about useful information and insights compared to businesses that solely rely on reports and tables.

Businesses that embrace node diagrams will notice their bottom lines improve.

Related Resources